ANYS,
A tensile testing machine plots Load versus the machine’s crosshead extension. That is the plot that you have above. In a tension test an extensometer is added to determine the yield point, but is normally removed after that.
You can “convert” to engineering Stress vs. extension or even to nominal strain by converting the nominal strain = (Lo + Extension)/Lo where Lo is the original Gauge Length (normally 2 inches or 1 inch, or 50 mm or 25 mm)
The %Elongation which is not a material property since it depends on the gauge length used in the test. The measured %Elongation for a 25 mm gauge length will by larger than for a 50 mm gauge length because it will reflect more the effect of the “necking” that develops after the Ultimate load is reached.
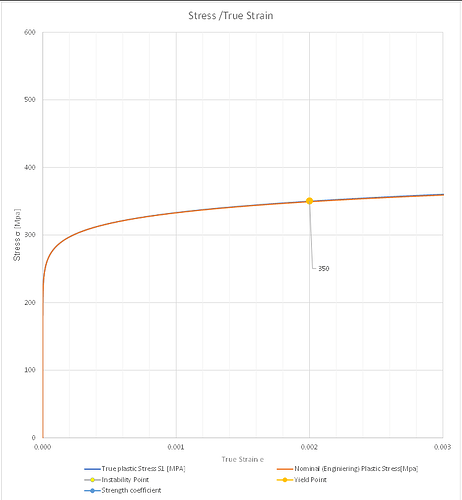
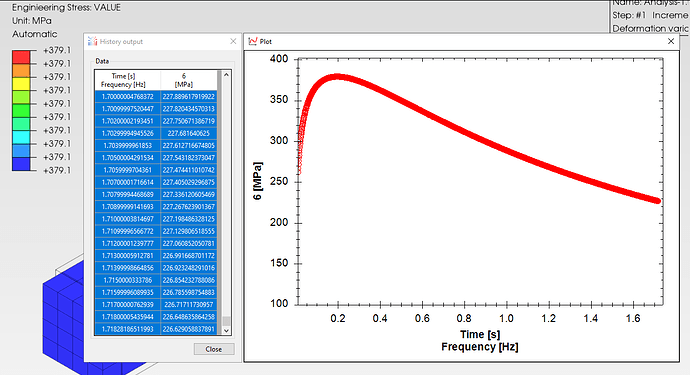
If the True stress (Li/Ai) where Li is the instantaneous load and Ai is the area corresponding to Li is plotted vs. the true strain defined as Ei = Ln(Ao/Ai) where Ao is the original cross sectional area, there will be no instability since the true stress will continue to increase as the cross sectional area decreases rapidly after the instability or maximum load is reached.
The instability that develops during a tensile test is well documented in the scientific literature, and when the Hollomon or Datsko Strain hardening equation is used to define the relationship between True Stress and True Deformation is used, the result is that the plastic deformation at instability, that is at the maximum load in a tension test equals m, the strain hardening exponent.
Datsko’s work clearly shows that if the Yield Strength and the Tensile Strength are known from a simple tension test, the the strain hardening exponent can be easily determined using my Excel suggestion or by trial and error using using the equations indicated.
I strongly disagree when the Blog states that determining m - the strain hardening exponent is difficult.
Furthermore, using the maximum elongation and matching it to the instability or point of maximum load simply shows poor understanding of mechanical properties of metals. I reiterate that the % reduction in area or %AR is the true measure of the ductility of the material. The fracture strain, which is used in metal forming plasticity Efracture = Ln (100/100-%AR) is the value that matters.
In Datsko’s book listed in my references Datsko writes that you can define the total strain as
Et = Ee +Ep (total strain equals Elastic def. plus Plastic Def)
Now if the deformation is only elastic, then
Ee = Stress/Young’s modulus = Sigma/E
And in the plastic portion
Et= Ee +Ep = (Sigma/Sigma_zero)^(1/m)
or Ep = (Sigma/Sigma_zero)^(1/m) - Sigma/E
this is the Ramberg–Osgood relationship and shows that the strain hardening exponent in the Ramberg–Osgood is simply the inverse of Datsko’s strain hardening exponent.
In his book, (I am trying to attach the plot in Log-Log coordinates) Datsko shows strain hardening curves for elastic plus plastic deformation and just the plastic deformation. The expected result is that when the plastic deformation is large the value of the elastic deformation does not affect the result of the calculation.
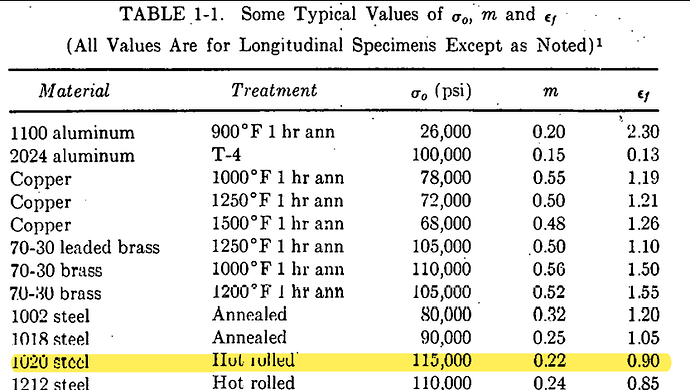
He points out that if the total strain is used for 1020 Steel ( I do not know where you are, but this is Carbon steel with .2% carbon) the curve fit is 120000 (Et)^0.22 and if Ep is used the equation is 121000 (Ep)^0.21. The numbers obtained for Et=0.002 and Ep=0.002 are approximately 30000 psi and 32000 psi. Obviously, for larger plastic deformation the values will be very similar if not identical.
ANYS, I sincerely hope that this comments have cleared some of your questions but feel free to contact me if you have more questions or ideas.
Best regards
Datsko’s-plot.zip (510.6 KB)
Et= Ee